[洛谷P4011]孤岛营救问题

发表于 | 分类于 | | 阅读次数:

题目

题目描述

$1944$ 年，特种兵麦克接到国防部的命令，要求立即赶赴太平洋上的一个孤岛，营救被敌军俘虏的大兵瑞恩。瑞恩被关押在一个迷宫里，迷宫地形复杂，但幸好麦克得到了迷宫的地形图。迷宫的外形是一个长方形，其南北方向被划分为 $N$ 行，东西方向被划分为 $M$ 列，于是整个迷宫被划分为 $N\times M$ 个单元。每一个单元的位置可用一个有序数对(单元的行号，单元的列号)来表示。南北或东西方向相邻的 $2$ 个单元之间可能互通，也可能有一扇锁着的门，或者是一堵不可逾越的墙。迷宫中有一些单元存放着钥匙，并且所有的门被分成 $P$ 类，打开同一类的门的钥匙相同，不同类门的钥匙不同。

大兵瑞恩被关押在迷宫的东南角，即 $(N,M)$ 单元里，并已经昏迷。迷宫只有一个入口，在西北角。也就是说，麦克可以直接进入 $(1,1)$ 单元。另外，麦克从一个单元移动到另一个相邻单元的时间为$1$ ，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。

试设计一个算法，帮助麦克以最快的方式到达瑞恩所在单元，营救大兵瑞恩。

输入格式

输出格式

将麦克营救到大兵瑞恩的最短时间的值输出。如果问题无解，则输出 -1 。

输入样例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1

输出样例

1
14

说明

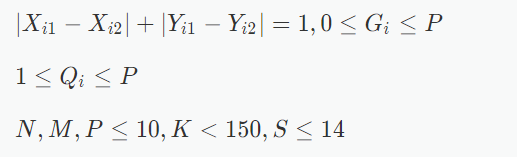
题解

基本方法

虽然它是网络流24题，但是其实根本不用网络流做。
首先我们来看看这个题目的数据范围，挺有意思的。
$N,M,P\le10$钥匙种类和地图大小都很小，嗯，感觉可以广搜，置于钥匙，我们就可以状态压缩一下

变量名 变量作用
$vis_{i,j,k}$ 记录你是否揣着$k$这个集合的钥匙到过$(i,j)$处
$map_{x1,y1,x2,y2}$ 表示$(x1,y1)$到$(x2,y2)$是个什么情况
$key_{i,j,k}$ 表示$(i,j)$存放的第$k$把钥匙
$num_{i,j}$ 表示在$(i,j)$处有几把钥匙
$tt$ 当前携带的钥匙集合

状态压缩

至于状态压缩的话，假设现在有5种钥匙，我们用1表示现在身上有，0没有。初始情况：

0 0 0 0 0

现在，我们来了第二把钥匙（从右往左）

0 0 0 1 0

这东西是不是很像二进制？
所以我们就可以用二进制来进行状压。
每次我们得到钥匙时，$tt|=1<<(key[i][j][k]-1)$
每次查询是否有第i把钥匙时，只要$tt\&(1<<(i-1))$为真，我们就可以认为有这把钥匙。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int dx[4] = { -1,1,0,0 };
const int dy[4] = { 0,0,-1,1 };
struct node {
	int x, y, step, key;
};
queue<node>q;
bool v[11][11][1 << 11];//v[x][y][tt]表示点(x,y)带有这么多的钥匙是否来过
int n, m, p, k;
int mp[11][11][11][11];//mp[x1][y1][x2][y2]表示两个点直接是否有墙或者是门，0表示可以直接通过
int key[11][11][11];//key[x][y][i]表示点（x,y）放的第i把钥匙
int num[11][11];//num[x][y]表示点（x,y)有多少把钥匙

int bfs() {
	int tt = 0;
	for (int i = 1; i <= num[1][1]; i++) {
		tt |= (1 << (key[1][1][i] - 1));//初始点可以放钥匙
	}
	v[1][1][tt] = 1;
	q.push((node) { 1, 1, 0, tt });
	while (!q.empty()) {
		node x = q.front(); q.pop();
		if (x.x == n && x.y == m) return x.step;
		for (int i = 0; i <= 3; i++) {
			int xx = x.x + dx[i];
			int yy = x.y + dy[i];
			if (1 <= xx && xx <= n && 1 <= yy && yy <= m) {//是否合法
				if (mp[x.x][x.y][xx][yy] == -1) continue;//墙，不能
				int t;
				if ((t = mp[x.x][x.y][xx][yy]) != 0)//门
					if ((x.key&(1 << (t - 1))) == 0) continue;//没有钥匙
				int tt = x.key;
				for (int j = 1; j <= num[xx][yy]; j++)
					tt = tt | (1 << (key[xx][yy][j] - 1));//带上钥匙
				if (v[xx][yy][tt]) continue;//同样的地点带着同样的钥匙，我们就认为状态重复了
				v[xx][yy][tt] = 1;
				q.push((node) { xx, yy, x.step + 1, tt });
			}
		}
	}
	return -1;
}

int main() {
	cin >> n >> m >> p >> k;
	for (int i = 1; i <= k; i++) {
		int x1, x2, y1, y2, g;
		scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &g);
		if (g == 0)mp[x1][y1][x2][y2] = mp[x2][y2][x1][y1] = -1;
		else mp[x1][y1][x2][y2] = mp[x2][y2][x1][y1] = g;
	}
	int s;
	scanf("%d", &s);
	for (int i = 1; i <= s; i++) {
		int x, y, p;
		scanf("%d%d%d", &x, &y, &p);
		key[x][y][++num[x][y]] = p;
	}
	printf("%d\n", bfs());
	return 0;
}